Grafo
Un grafo è una struttura matematica costituita da nodi o vertici e archi che li collegano. La teoria dei grafi è un parte importante della combinatoria, usata in topologia, teoria degli automi, geometria dei poliedri, informatica (algoritmi, circuiti, reti di computer, mappe di siti). I grafi sono alla base di modelli di sistemi e processi studiati nell’ingegneria, nella chimica, nella biologia molecolare, nella ricerca operativa, nella organizzazione aziendale, nella geografia (sistemi fluviali, reti stradali, trasporti), nella linguistica strutturale, nella storia (alberi genealogici, filologia dei testi).
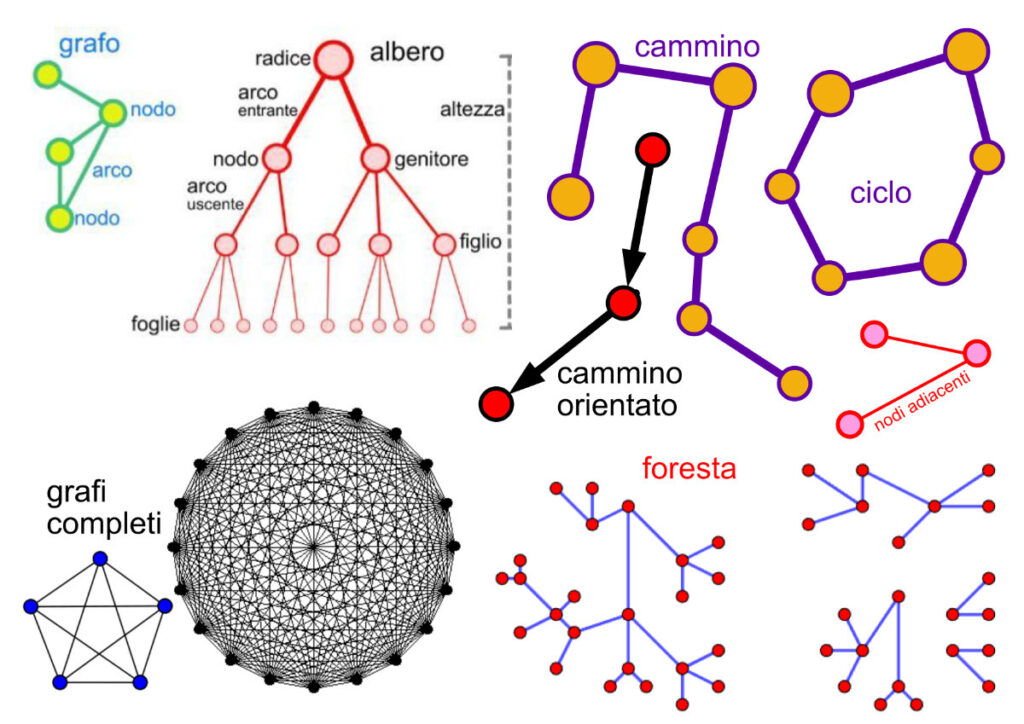
Un grafo è un insieme costituito da due sottoinsiemi, il sottoinsieme dei nodi o vertici, e il sottoinsieme degli archi, detti anche lati o spigoli, che collegano fra loro i nodi. Il numero degli archi determina la dimensione del grafo. Un grafo è orientato se gli archi hanno una direzione logica rappresentata da frecce, altrimenti è non orientato. La differenza tra grafi orientati e non orientati in informatica è importante nello sviluppo dell’algoritmo di calcolo per elaborare la rete dei nodi del grafo, perché la complessità dell’algoritmo è molto diversa. Il grafo orientato può essere chiamato anche grafico diretto o digrafo.
Due nodi sono adiacenti se sono congiunti da un arco. Una successione di nodi è costituita da un certo numero di nodi adiacenti a due a due collegati tra loro; un cammino è una successione che non contiene due volte lo stesso lato. Un cammino è semplice se contiene tutti nodi distinti. Se un cammino congiunge un nodo con se stesso si chiama ciclo o circuito. Un grafo si dice connesso quando due punti qualsiasi che ne fanno parte possono essere congiunti da un cammino. Un cammino orientato è un percorso in un grafico orientato, un ciclo orientato è un percorso che termina col nodo di partenza.
Un grafo non orientato, connesso e privo di cicli si chiama albero. Se si aggiunge uno spigolo si crea un ciclo, se si toglie si perde la connessione. Un albero non connesso o un insieme di più alberi si chiama foresta. Un albero con radice ha un nodo iniziale che non ha archi entranti e che costituisce un vertice raggiungibile da qualsiasi altro vertice con un solo cammino. Ogni nodo dell’albero può avere un solo arco di entrata e più archi di uscita. Se gli archi sono orientati il nodo a monte è un nodo padre, il nodo a valle è un nodo figlio. Se un nodo non ha archi in uscita si chiama foglia. L’albero con radice è molto usato in informatica, per esempio per rappresentare la struttura di un sito web, o nella struttura di un organigramma o di una mappa mentale.
Un grafo è completo se ogni nodo è adiacente ad ogni altro.
Grafi, reti semantiche, mappe concettuali
I grafi sono gli elementi costitutivi delle reti, che hanno vari aspetti e funzioni a seconda del tipo di relazioni fra i nodi, ossia di che cosa succede lungo gli archi. Fra esse troviamo le reti di Petri e le reti semantiche, da cui derivano le mappe concettuali. Le mappe mentali semplificano quelle concettuali adottando una rete con un grande hub centrale, da cui si diramano hub e nodi periferici. Mappe concettuali e mentali con l’informatica diventano ipermappe interattive e multimediali.
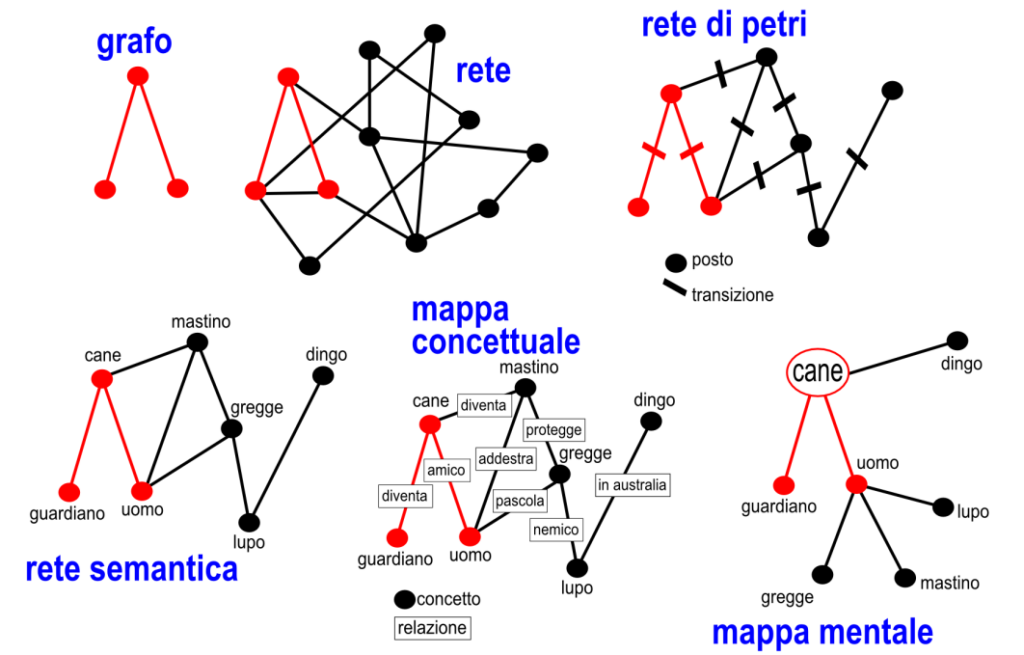
Le reti sono serie di componenti, sistemi o entità interconnessi tra di loro. Sono informatiche, di telecomunicazione, stradali, sociali, biologiche, in altre parole qualsiasi sistema di elementi interconnessi, dal sistema nervoso alle organizzazioni terroristiche. Le reti possono essere policentriche, a stella, ad anello. I nodi che hanno molte connessioni si chiamano hub, e sono i più importanti della rete, quelli che influiscono di più sulla rete intera e su altri nodi.
Le Reti di Petri, dette anche reti posto/transizione o reti PT, sono rappresentazioni matematiche che descrivono la struttura di un sistema distribuito come un grafo che ha nodi detti “posti”, nodi detti “transizioni”, archi che collegano posti e transizioni. Un posto dà luogo ad un evento (transizione) che influisce su un altro posto modificandolo. Possono esserci archi tra posti e transizioni, ma non tra posti e posti (mancherebbero gli eventi) o transizioni e transizioni (mancherebbero gli elementi interessati agli eventi). Un posto da cui un arco parte per finire in una transizione è detto posto di input della transizione; un posto in cui un arco arriva partendo da una transizione è detto posto di output della transizione.
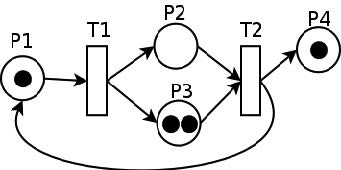
In questa rete TP il posto P1 genera l’evento T1 che trasforma i posti P2 e P3, che a loro volta producono la trasformazione T2 che agisce sul posto P4, concludendo il processo, e su P1, introducendo nella rete una procedura ricorsiva. Questo tipo di rete è la base teoprica di rappresentazioni grafiche di processi come i flow chart e il PERT. Le reti di Petri si usano in ingegneria informatica, workflow management, data analysis, programmazione, affidabilità, diagnosi in intelligenza artificiale.
Una rete semantica è una forma di rappresentazione della conoscenza come grafo orientato formato da vertici, che rappresentano concetti, e archi, che rappresentano relazioni semantiche tra i concetti. Il modello è usato per dizionari elettronici, ipertesti, mappe concettuali. Le reti semantiche si basano sempre sui nodi e i link, ma li qualificano, in quanto un nodo può rappresentare un concetto, un sostantivo, un insieme, e un altro nodo può essere una specializzazione o generalizzazione del precedente, un iponimo o un iperonimo, un sottoinsieme o un sovrainsieme.
Mappe concettuali e mentali, flow chart e organigrammi sono applicazioni particolari di grafi e reti semantiche.

