Frattale
Un frattale è un oggetto geometrico che, replicandosi con forme e dimensioni leggermente modificate, genera strutture estremamente complesse.
Si considera frattale un insieme, diverso dagli usuali oggetti geometrici, con le seguenti proprietà:
- Autosimilarità: il frattale si sviluppa replicando se stesso a scale e con colori differenti, in modo che i suoi particolari più minuti hanno la stessa struttura formale della figura intera, anche se può apparire dilatata o compressa in base alle variazioni impresse nell’algoritmo di ripetizione. La ricorsività fa parte dell’autosimilarità: il frattale è l’applicazione di una formula che si ripete modificandosi in base all’output che diventa input per la ripetizione successiva. In tal modo il frattale può raggiungere un livello infinito di complessità.
- Struttura fine: il frattale rivela dettagli ad ogni ingrandimento.
- Irregolarità: il frattale non può essere descritto come luogo dei punti che soddisfano semplici condizioni geometriche o analitiche come triangoli o tangenti.
Dimensione non intera: come dice il nome, un frattale non ha dimensioni intere (linea = 1, quadrato = 2, cubo = 3) ma frazionarie (curva di Koch = 1,26).
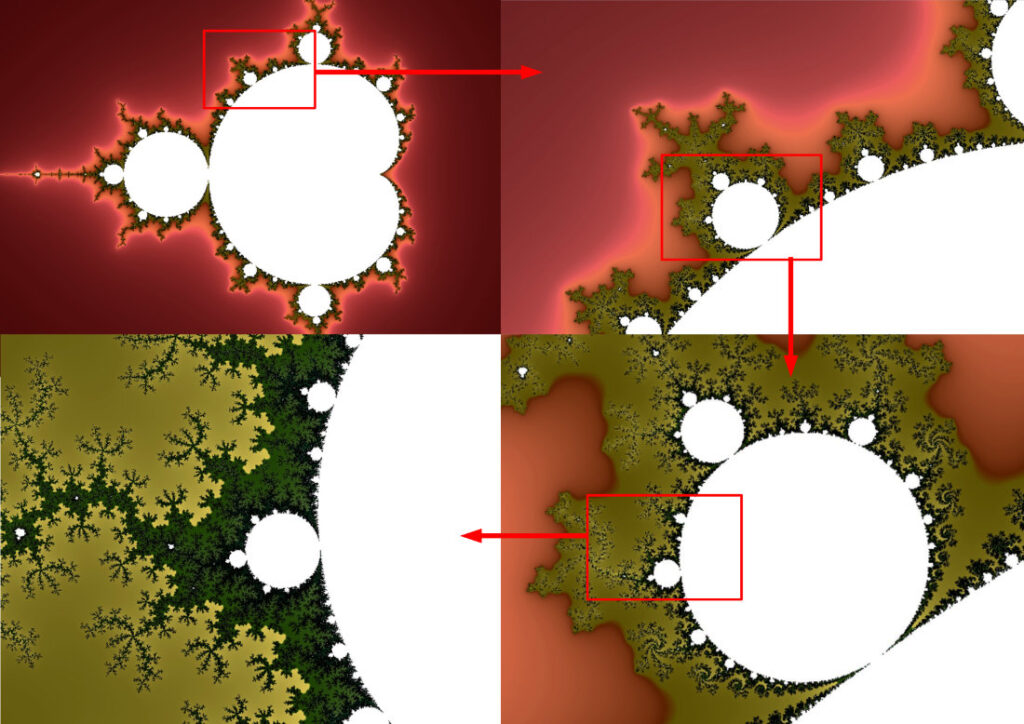
L’autosimilarità si vede bene ingrandendo una figura di Mandelbrot. In senso orario, l’immagine mostra in alto a sinistra l’insieme, in alto a destra l’ingrandimento della parte bordata in rosso, il cui particolare è ingrandito in basso a destra, fino all’ingrandimento del particolare di questo, in basso a sinistra. E si potrebbe continuare a ingrandire, sempre con gli stessi risultati, verificando la caratteristica della struttura fine.
Per comprendere come funziona un frattale osserviamo quattro modelli fondamentali, l’insieme di Cantor, la curva di Koch, il triangolo di Sierpinski, la spugna di Menger. Con essi si comprende come da forme semplici si arrivi a forme assai complesse solo con poche iterazioni, e come sia possibile ottenere i frattali più fantasiosi per forme e colori, e per modelli matematici e grafici che replicano gli stessi comportamenti che in natura danno forma a montagne, fiumi, nuvole, fiocchi di neve, alberi, piante e fiori, stormi di uccelli e sciami di api e di farfalle.

Insieme di Cantor
E’ un insieme di segmenti in cui si parte da un segmento, lo si divide in tre parti uguali, si elimina la parte mediana. Si ripete la stessa operazione sui due segmenti che restano, e così via, fino ad ottenere segmenti piccolissimi la cui texture è detta anche “polvere di Cantor”, dal nome di Georg Cantor, il padre della Teoria degli Insiemi.
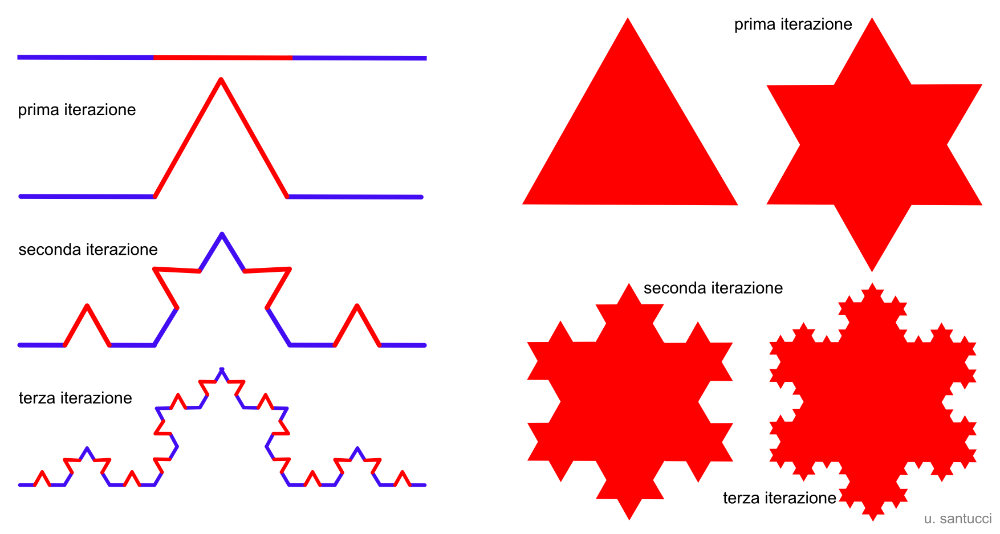
Curva di Koch
La curva di Koch ha una procedura simile a quella dell’insieme di Cantor. Si parte da un segmento, lo si divide in tre parti, si duplica la parte mediana e la si ruota a formare un triangolo equilatero. Si continua con lo stesso procedimento per ogni lato del triangolo.

Triangolo di Sierpinski
Si parte da un triangolo equilatero, lo si divide in quattro triangoli equilateri, si toglie il triangolo centrale. Si continua così per ognuno dei tre triangoli, all’infinito.

Spugna di Menger
Si parte da un cubo regolare, lo si divide in 9 sottocubi regolari, si tolgono tutti i sottocubi centrali, si ripete l’operazione per ciascuno dei sottocubi rimasti.
Come si vede, questi frattali applicano tutti e quattro lo stesso tipo di procedura: dividi per tre, togli uno e riduci. Altri tipi seguono altre procedure, come il sistema di Lindenmayer con cui si costruiscono forme ad albero simmetriche o distorte, come in questo esempio in cui l’elemento di partenza è la rappresentazione geometrica del teorema di Pitagora.

Albero di Pitagora
L’albero è stato ideato e disegnato a mano nel 1946 dall’ingegnere olandese Albert Bosman. A seconda se si parte da un triangolo rettangolo isoscele o scaleno si ottengono sviluppi diversi ad albero, i cui rami descrivono spirali logaritmiche. Il frattale a sinistra si sviluppa con angoli di 45°, l’albero di destra con angoli di 30° e 60°, il centrale con angoli casuali.
I frattali possono essere deterministici e aleatori o stocastici.
I frattali deterministici sono generati da algoritmi che si ripetono sempre nello stesso modo e non ammettono variabili aleatorie, quindi le iterazioni sono prevedibili. Sono lineari e non lineari. I frattali lineari sono costruiti con algoritmi di tipo lineare, ossia con ingrandimenti e riduzioni dell’elemento iniziale. Vanno indicati i fattori di riduzione, e le immagini ridotte possono essere collocate in qualsiasi posizione. La figura può quindi essere spostata, allungata, accorciata, riflessa, ruotata o trasformata in tutti i modi, purché le varie trasformazioni risultino essere delle omotetie e i segmenti di retta dell’originale rimangano dunque segmenti di retta. La forma frattale è data dal meccanismo di feedback che utilizza la forma modificata come input per la trasformazione successiva. I frattali di Cantor, Koch, Sierpinsky, Menger, sono tutti frattali lineari.

I frattali non lineari sono costruiti con algoritmi non lineari come le equazioni esponenziali, logaritmiche, trigonometriche. Ad essi appartengono i frattali derivati dal diagramma di Feigenbaum, come quelli classici di Julia e di Mandelbrot.
Come si vede, le procedure sono tutte molto semplici, ma generano complessità ad ogni ripetizione che agisce su ciò che è già stato modificato dalla ripetizione precedente. Un esempio classico di generazione caotica dalla ripetizione di un’operazione semplice è il diagramma di Feigenbaum che all’inizio presenta una sola biforcazione, e poi continua con biforcazioni in progressione geometrica.
I frattali aleatori introducono nelle iterazioni elementi casuali non prevedibili, come numeri random inseriti nella formula generatrice. Per comprendere la differenza fra un frattale deterministico e un frattale aleatorio confrontiamo un albero di Lindenmayer con un pino marittimo naturale.

L’albero frattale costruito con le biforcazaioni di Lindermayer è prevedibile, perché tutte le biforcazioni hanno lo stesso angolo e lo stesso rapporto di riduzione di dimensione. Anche andando verso la cima, ossia verso il più alto livello di complessità, la forma delle biforcazioni resta omotetica, ossia simile alla prima biforcazione. L’albero naturale cresce con lo stesso principio di biforcazione e riduzione, ma durante il processo di crescita intervengono variabili casuali a modificare la forma di rami e foglie, come vento, fulmini, nidi di uccelli ed insetti, esposizione al sole, e così via. I frattali stocastici si comportano nello stesso modo, anche se con variabili ridotte, e perciò sono più adatti a simulare forme naturali come montagne, nuvole o piante, ma anche immagini fantastiche e scenari immaginari.

In alto il frattale aleatorio simula un paesaggio montano con la vegetazione che si modifica con la quota e con le nevi che si sciolgono formando i fiumi. In basso un paesaggio fantastico dove le iterazioni frattali si comportano come stalattiti e stalagmiti, ma anche come cupole e guglie di templi orientali.
Arte frattale
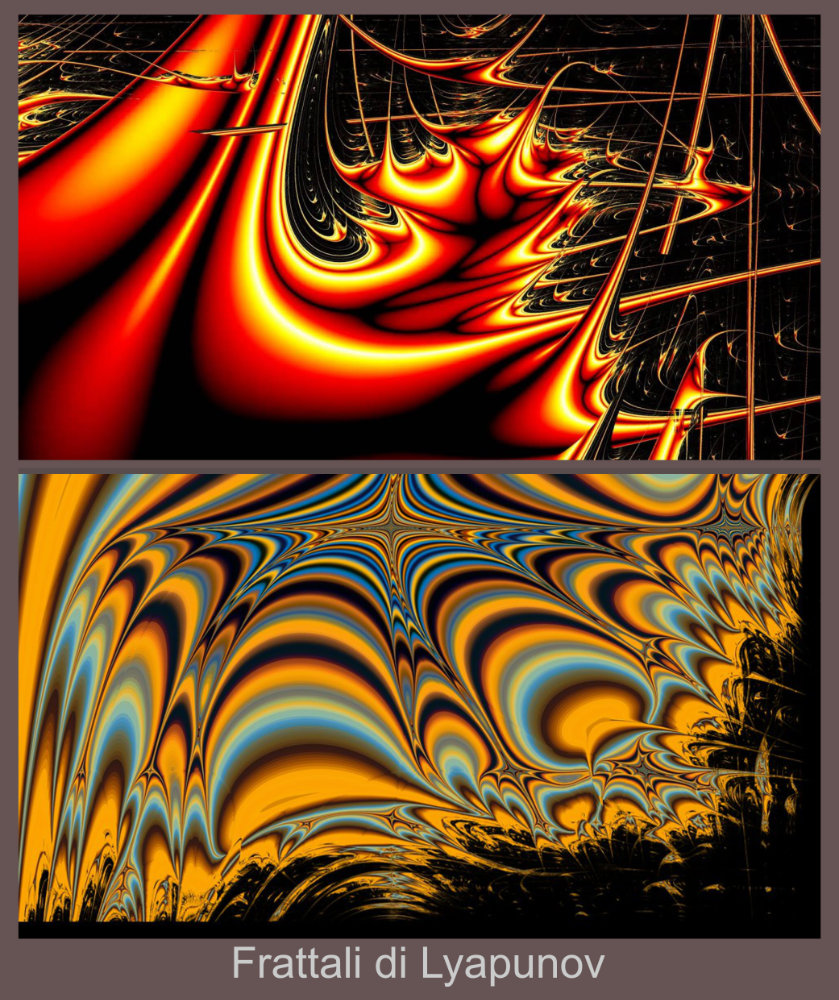
I frattali sono ampiamente usati nella ricerca artistica e nella produzione di immagini fisse e di animazioni per illustrazioni, effetti speciali video e cinematografici, grafica 3D. Il problema che si sono posto artisti e ricercatori è la generazione automatica di immagini, specialmente quando si devono replicare gli stessi elementi grafici per fare texture, folle di persone, sciami di volatili, foglie di alberi, effetti di nuvole, pioggia e neve, nel caso di simulazioni realistiche, oppure di ottenere immagini che non si possano fare in altro modo che con il calcolo dei computer, come i paesaggi immaginari e fantascientifici, i frattali di Lyapunov che producono bellissime immagini grazie alle diverse combinazioni di sequenze fra valori positivi per zone di stabilità e negativi per zone di caos, a cui si attribuiscono valori di luminosità e di colori, in modo da simulare effetti tridimensionali, e i frattali del tipo burning ship e flame.

Problem solving
Mentre noi ci attardavamo con le figure perfette della geometria di Euclide, la Natura giocava con i frattali. Dietro le forme irregolari di monti, fiumi, conchiglie e fiori, essi celavano rigorose equazioni matematiche che non potevano essere studiate con la geometria euclidea.
Il problema che si pose Benoît Mandelbrot, che per primo parlò di “frattali” negli anni ’60 del secolo scorso, fu come misurare forme naturali non riconducibili a oggetti geometrici euclidei. “Le nuvole non sono sfere, le montagne non sono coni”, diceva Mandelbrot mentre pensava a come modellizzare e misurare le coste inglesi, che man mano che si riduce la scala presentano nuove curve e profili sempre più frastagliati. Lo stesso avviene per tutto ciò che fa la natura, dalle rocce agli alberi, fino a quello che sarà l’emblema del frattale naturale, il broccolo romano che ripete la stessa struttura fin nei particolari più minuti.
I frattali dunque sono spesso utilizzati per modellizzare i processi caotici, che nonostante abbiano un comportamento apparentemente casuale, presentano in dettaglio delle caratteristiche di autosimilarità, come gli sciami di uccelli o di api, le nuvole e in genere i fenomeni meteorologici, il vulcanesimo, ma anche il comportamento di mercati, finanza, fenomeni sociali come migrazioni o pandemie. La scienza dei frattali non si limita quindi soltanto a generare complesse immagini grafiche mediante i computer, ma fornisce strumenti che permettono di creare modelli di fenomeni complessi, con precisione in alcuni casi maggiore dei modelli tradizionali della matematica e della fisica.
C’è uno stretto legame tra frattali e teorie del caos. I regimi sociali sono difficili da governare, per cui ci si deve affidare alla autoregolazione dei sistemi complessi. I frattali offrono modelli di sistemi complessi in cui la parte è simile al tutto, e l’insieme generale è determinato dalle iterazioni delle parti che si autoregolano in base a regole semplici ma ricorsive.
In un sistema sociale come può essere una città o un quartiere, oppure un’azienda o un’organizzazione, agiscono due forze antitetiche: l’autonomia di individui e gruppi, che agisce dal basso, e la pianificazione che agisce dall’alto. La contraddizione può essere compresa e governata proprio con la geometria frattale e la teoria dei sistemi non lineari auto-organizzati che si sviluppano in base a regole, costanti e variabili che è possibile pianificare.

Il famoso frattale di Mandelbrot detto “La valle delle proboscidi“, basato sul semplice algoritmo secondo cui l’iterazione avviene col quadrato della situazione attuale più una cosatante, è una buona metafora visiva di passaggio dal pensiero lineare semplicistico al pensiero sistemico complesso, e rappresenta bene il modello di organizzazione caordica, in cui coesistono lo sviluppo (fare meglio le solite cose) con l’innovazione (introdurre diversità e varianti). E’ un modello complesso che rappresenta un’organizzazione basata sulla dinamica sistemica di incremento e riduzione (effetto valanga e bilancia), con intelligenza e leadership distribuita e caordica, ossia sull’orlo del caos, in cui non si può ordinare e prevedere tutto, ma è meglio lasciar fare e osservare gli sviluppi per ottenere discontinuità e quindi innovazione (le biforcazioni del sistema di Feigenbaum che sono finestre sulle possibili opportunità e minacce). Un’organizzazione che apprende, in cui piccole cause producono grandi effetti con l’iterazione modificante (effetto farfalla o effetto colpo di frusta), e che si basa su team motivati, autonomi e responsabili che si muovono con regole semplici e minime. L’autoorganizzazione delle imprese e delle unità produttive è simile a quella degli organismi viventi che si adattano all’ambiente con intelligenza dinamica.
I frattali si prestano a molti impieghi, in tutti i casi in cui bisogna modellizzare sistemi che si comportano in modo caordico, sull’orlo in cui convivono ordine e caos, in cui piccole cause producono grandi effetti, come azioni di singole persone che si propagano in reti interconnesse, dalle informazioni alle pandemie, dalla mobilità urbana ed extraurbana alla finanza internazionale, dalla meteorologia allo studio delle galassie, dalla medicina alla bioingegneria.
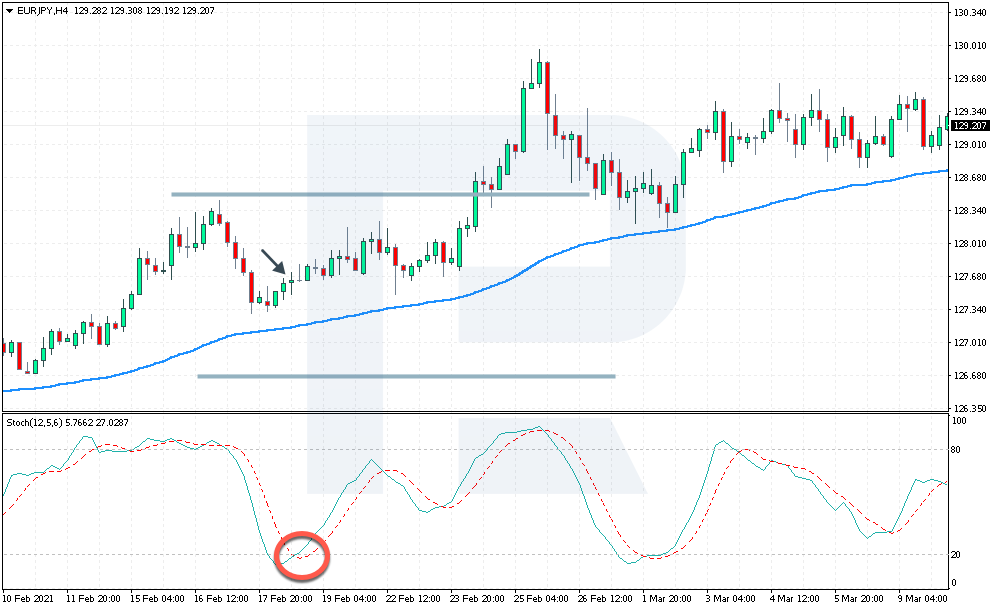
Per osservare i movimenti borsistici i finanzieri usano oscillatori stocastici con grafici a candele che, visualizzando le oscillazioni dei valori che avvengono durante le contrattazioni borsistiche, utilizzano formule frattali, utili anche a fare previsioni e costruire modelli di mercati finanziari. Nell’esempio mostrato si vede in basso la curva generale, e in alto un particolare della stessa con le candele che visualizzano i valori azionari massimi e minimi ad apertura e chiusura delle contrattazioni.
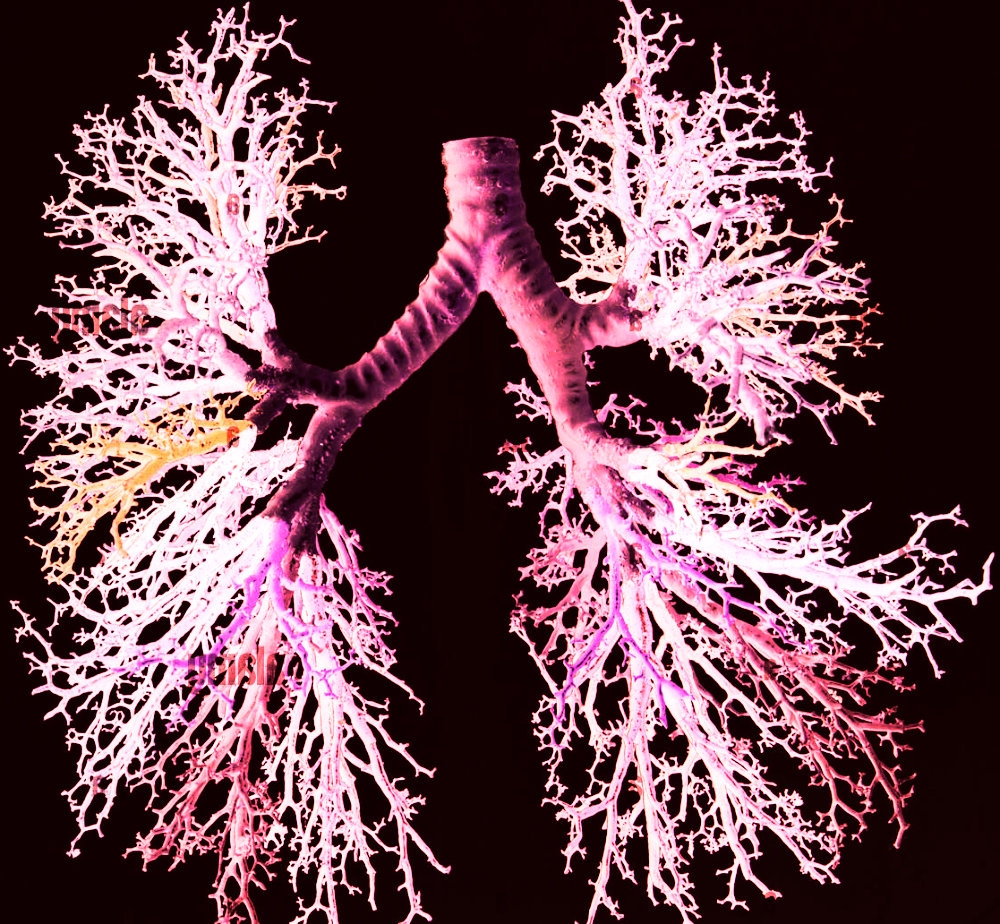
Il modello 3D di albero bronchiale mostra la tipica struttura frattale a biforcazioni successive. Fa riflettere il fatto che i rami di un albero vegetale, fatti per produrre ossigeno, abbiano la stessa struttura dei rami di bronchi e polmoni che ci servono per respirare ossigeno.

Secondo alcune teorie cosmologiche tutto l’universo sarebbe un frattale, comunque la geometria frattale ben si presta a studiare le forme di galassie e ammassi stellari, sia con simulazioni e modelli matematici, sia con osservazioni fatte con i supertelescopi terrestri e spaziali.

